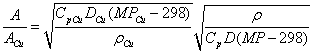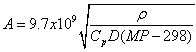Justification for equations in suggested NFPA 780 Chapter 8 revisions

Ewen Thomson Jan 17,2007

8.4.1 Main Conductor.

8.4.1.1 A main conductor made of copper shall have a cross sectional area of at least 21 mm² (0.033 in²).

8.4.1.2 A main conductor made of aluminum shall have a cross sectional area of at least 40 mm² (0.062 in²).

*8.4.1.3 A conducting fitting constructed of metal other than copper or aluminum that neither contains electrical wiring, nor connects conductors containing electrical wiring, shall be permitted to be used as a main conductor if it has at least the cross sectional area given by the formula:

mm²

where C_p is the specific heat capacity in J kg^-2 K^-1, D is the density in kg m^-3, ρ is the resistivity in Ω m, and MP is the melting point in degrees Kelvin.

A8.4.1.3 If a metal with the area given by the equation in Section 8.4.1.3, is subject to the lightning heating (action integral) required to raise the temperature of a copper conductor with 21 mm² (0.033 in²) from a nominal temperature of 298 K to the melting point of copper, then its temperature would be raised to the melting point of the metal. Values for silicon bronze and stainless steel are given in the table below.

Metal	Cp J kg^-2K^-1	D kg m^-3	Ρ Ω m	MP K	Area mm^2
Silicon bronze	360	8800	2.55x10^-7	1356	85
Stainless steel	510	7930	9.6x10^-7	1800	125

Table A8.4.1.3 Areas for main conductor not containing electrical wiring

Note that conductors with these areas have a larger resistance per unit length than a main conductor made of copper and so should not be used where potential equalization is required.

Justification

The ohmic heating in the conductor causes a temperature rise ΔT according to

where m is the mass of a length L of the conductor. Ignoring skin effects, that is, assuming that the current density is uniform across the area,

and

where D is the density. Hence the action integral for a particular metal is related to the other parameters by

If we assume the same action integral for the same length of two different conductors and consider ΔT to be the melting point, MP, less the ambient temperature (assumed to be 298K), then we can find the corresponding ratio of the squares of the areas. Since copper conductors are the reference, the area for a different metal is given by

where the "Cu" subscript denotes copper. The following values are representative of various metals commonly used in the marine industry:

Metal	Copper	Aluminum	Silicon bronze	Stainless steel
Cp J.kg^-2.K^-1	385	913	360	510
D kg.m^-3	8930	2710	8800	7930
ρ Ω.m	1.7x10^-8	2.65x10^-8	2.55x10^-7	9.6x10^-7
MP K	1356	932	1356	1800

For A_Cu=21 mm², we get

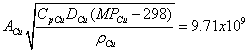
Hence we get

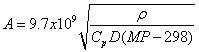
as above.

This analysis gives the same results as that used by Baatz (1977) (Baatz, H. "Protection of Structures" in Golde, R.H. (ed.) Lightning: Volume 2, pp 599-632.) Other researchers (for example Golde, R.H., Protection of structures against lightning, IEE Control and Science, 115, 1523-1529,1968) also take account of the skin effect that gives rise to a relatively larger resistance for copper, which has a smaller skin depth than the other metals considered here. Hence the values are conservative.

*8.4.1.4 A conducting fitting constructed of metal other than copper or aluminum that either contains electrical wiring or connects conductors containing electrical wiring shall be permitted to be used as a main conductor if it has the same or smaller DC resistance per unit length as a copper conductor with a cross sectional area of 21 mm² (0.033 in²).

A8.4.1.4 The area of a conductor of uniform cross section that has the same resistance as a copper conductor of area A_Cu is given by:

where ρ_Cu=1.7x10^-8Ωm is the resistivity of copper, and A_Cu=21 mm² for a main conductor. Using the same parameters in Table A8.4.1.3, the areas are 315 mm² (0.49 in²) for silicon bronze and 1200 mm² (1.8 in²) for stainless steel.

Justification

In this case we equate the resistances for the same length so that

The above follows directly. Note that this area for aluminum (33 mm²) is less than the area that raises its temperature to the melting point (40 mm²). For silicon bronze and stainless steel it is considerably larger.

8.4.6 Connecting fittings

8.4.6.1 Fittings of any length that are made of aluminum shall be permitted to join two conductors if the minimum cross sectional area meets the requirements of Section 8.4.1 for main conductors or 8.4.2 for bonding conductors.

*8.4.6.2 Connecting fittings made of metals other than aluminum or copper shall either;

1. have the same resistance per unit length as the corresponding type of conductor (that is, main or bonding); or;

2. have a cross sectional area at least as large as that given in Section 8.4.1.3 for a main conductor or Section 8.4.2.3 for a bonding conductor, and have a resistance that is not more than the resistance of 61 cm (2 ft) of the corresponding copper conductor.

A8.4.6.2

1. The area of a conductor of uniform cross section that has the same resistance per unit length as a main conductor is given by the equation in A8.4.1.4. For connecting a main conductor, the areas are 315 mm² (0.49 in²) for silicon bronze and 1200 mm² (1.8 in²) for stainless steel. For connecting a bonding conductor the required areas are 125 mm² (0.19 in²) for silicon bronze and 470 mm² (0.73 in²) for stainless steel.

2. Equating resistances for a copper conductor of area A_Cu, resistivity ρ_Cu, and length L_Cu and a metal connector of area A, resistivity ρ_, and length L gives a maximum allowable length for the metal connector of:

The length is the same for both main and bonding conductors and is 16 cm (6.5 in) for silicon bronze and 6.3 cm (2.5 in) for stainless steel when L_Cu=61 cm (2 ft).

Justification

Using different metals for connections is important for bonding conducting fittings such as lifeline stanchions, railings, handrails, etc. Typically the fitting is attached using stainless steel or silicon bronze bolts and so the practical concern is what size bolt can also function as a connection. The areas required for the same resistance per unit length as copper are impractically large: hence the need for a compromise based on the same thermal effects as the corresponding copper conductor. It is not clear where the length of 61 cm (2 ft) originates. The resistance of 61 cm of 21 mm² copper is 0.5 mΩ, corresponding to a voltage drop of 15V across a connection with a current of 30kA flowing. This is too small to initiate a sideflash but could be a concern for a low-voltage circuit. However, the main application for this is typically bonding where the expected currents are much lower, perhaps orders of magnitude. The derivation of the values in A8.4.6.2 are found by equating resistances. This is independent of A because it appears as the ratio A/A_Cu, and, (from above)